Help - Ingranaggi a Denti Dritti
Ingranaggi a Denti Dritti è una applicazione che genera per inviluppo ruote dentate a denti dritti
mettendo a disposizione le seguenti funzionalità:
- calcolo dei parametri geometrici della ruota,
- disegno della ruota con dettaglio della dentatura,
- modifica dello spessore del dente mediante correzione (ottimizzazione della dentatura),
- calcolo dello sforzo massimo a flessione alla base del dente attraverso il metodo di Lewis,
- creazione di un file DXF con il profilo 2D della ruota dentata, utilizzabile con qualunque software CAD 2D o 3D.
Qui è possibile trovare una chiara spiegazione del significato dei termini utilizzati nel software oltre ad informazioni aggiuntive sulle ruote dentate a denti dritti, come formule, un esempio numerico, un'utile bibliografia e alcuni consigli sulla correzione delle ruote dentate.
La figura #1 contiene una rappresentazione dei termini riguardanti le ruote dentate e il calcolo dello sforzo massimo a flessione alla base del dente.
#1 - Dettaglio di una ruota dentata a denti dritti
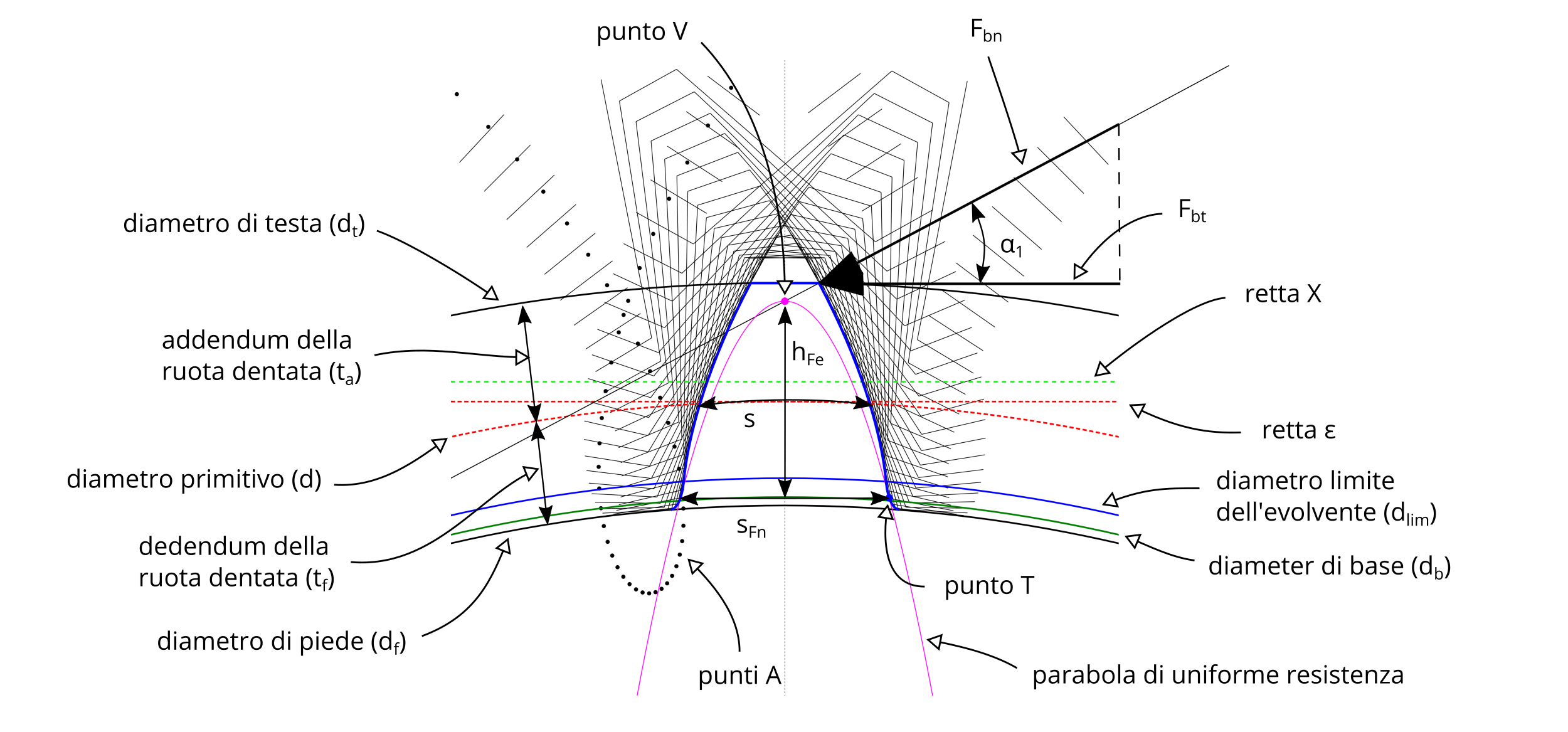
Nella figura #2 c'è lo schema utilizzato per creare per inviluppo il profilo del dente di una ruota dentata a denti dritti.
#2 - Schema per creare per inviluppo una ruota dentata
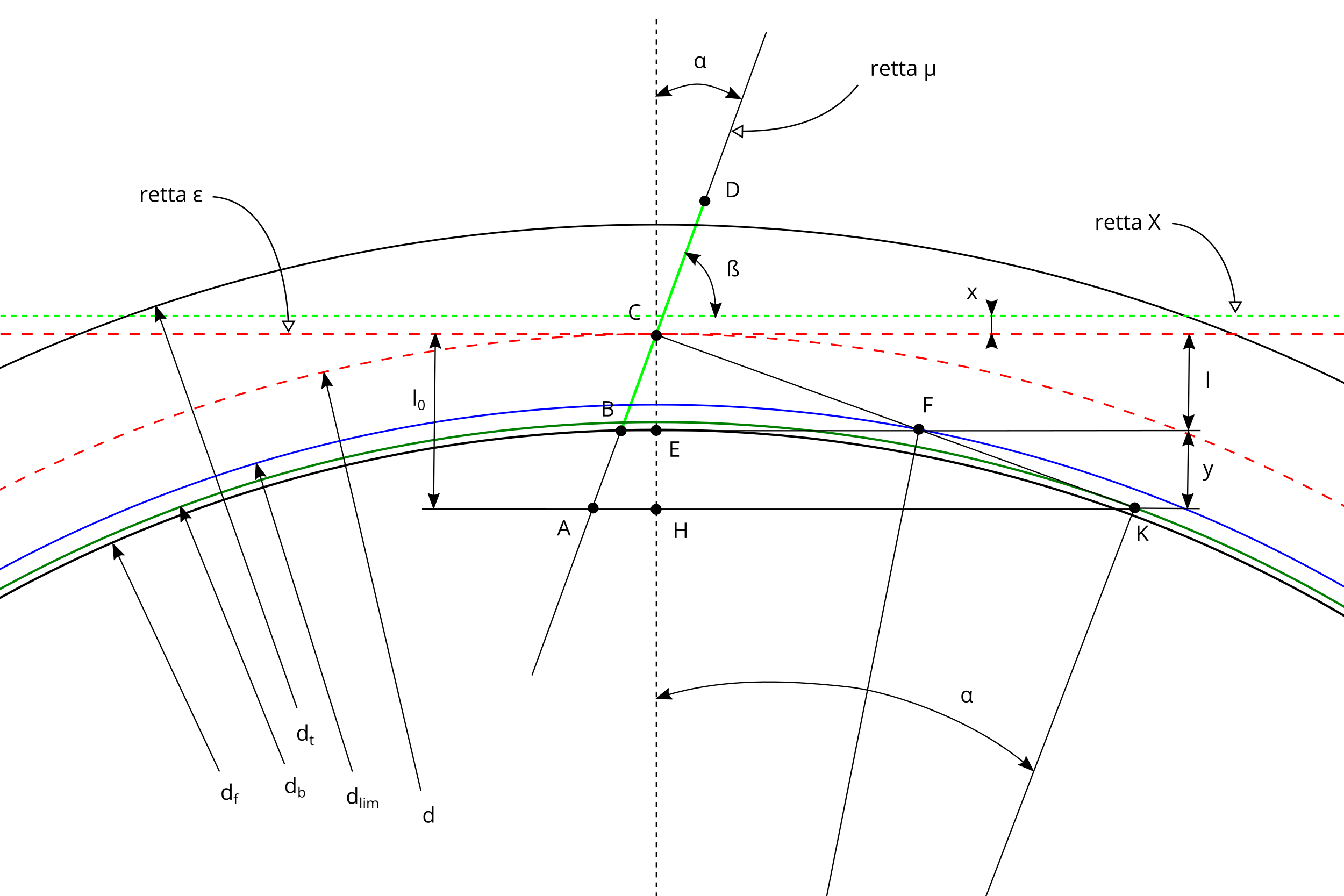
La figura #3 rappresenta l'utensile dentiera utilizzato per generare la ruota dentata, come definito nella norma ISO 53:1998.
#3 - Utensile dentiera
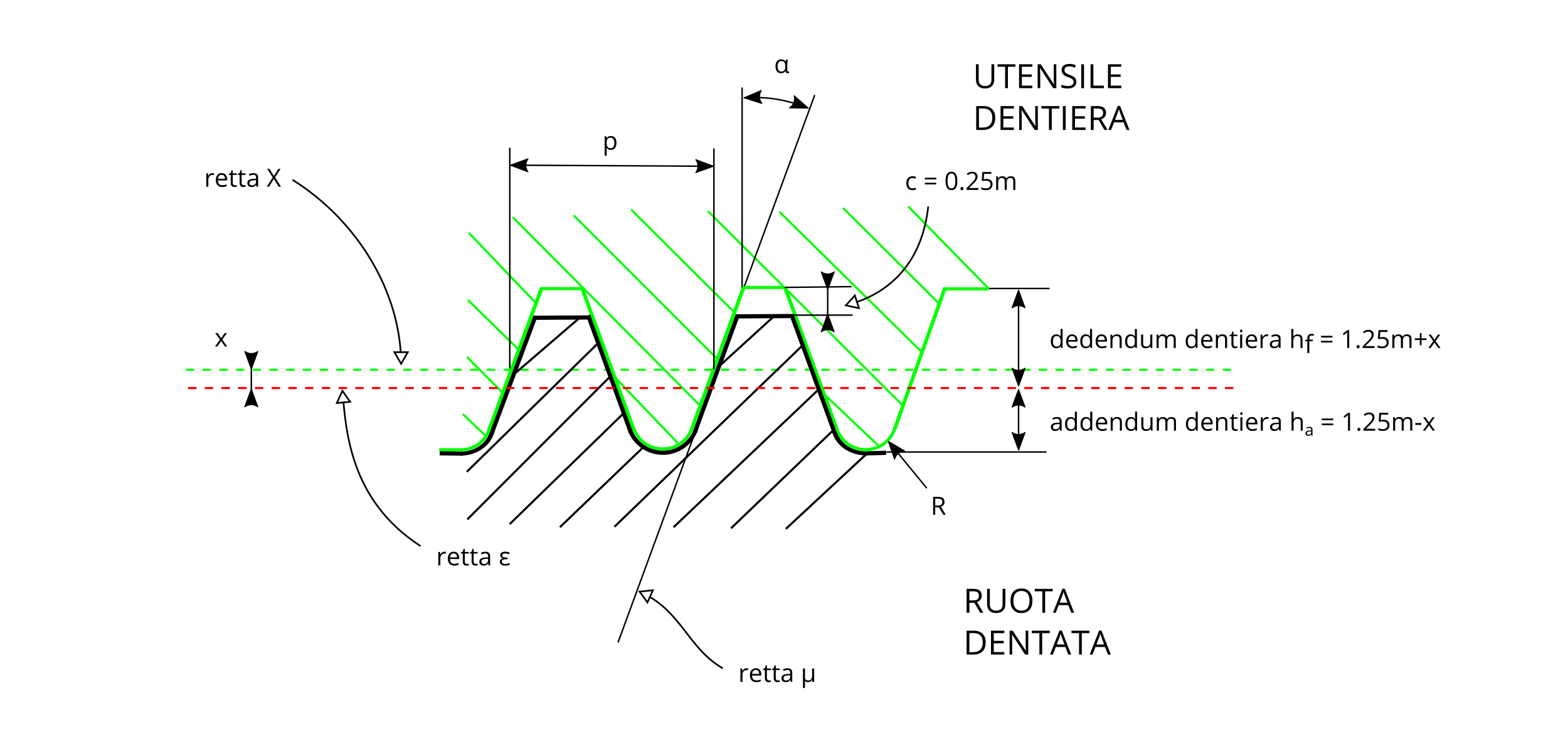
La tabella sotto riportata contiene un esempio numerico e alcune formule riguardanti le ruote dentate a denti dritti, valide quando R/m = 0 e x/m = 0.
| Elemento | Formula | Esempio |
| numero di denti | $$z$$ | 30 |
| modulo | $$m$$ | 5 mm |
| angolo di pressione | $$ \alpha $$ | 20° |
| coefficiente di correzione | $$ x/m $$ | 0 |
| coefficiente di raggiatura dell'utensile dentiera | $$ R/m $$ | 0 |
| coppia statica nominale | $$ C $$ | 250 Nm |
| spessore del dente | $$ b $$ | 10 mm |
| $$ l_0 = \frac{d} {2} \cdot {sin}^2(\alpha)$$ | 8.77 mm | |
| $$ \frac{y} {d/2} = \frac{2.5} {z} - {sin}^2(\alpha)$$ | -0.0336 | |
| $$ l = l_0 + y$$ | 6.25 mm | |
| passo | $$p = {m \cdot \pi}$$ | 15.71 mm |
| diametro primitivo | $$d = {m \cdot z}$$ | 150 mm |
| diametro di base | $$d_b = d \cdot cos(\alpha)$$ | 140.95 mm |
| diametro limite dell'evolvente | $$d_{lim} = 2 \cdot \sqrt{ \left( r-l \right)^2+\left( \frac{l}{tan(\alpha)}\right)^2}$$ | 141.72 mm |
| diametro di piede | $$d_f = d - 2 \cdot l$$ | 137.5 mm |
| diametro di testa | $$d_t = d + 2 \cdot m $$ | 160 mm |
| addendum della ruota dentata | $$t_a = m $$ | 5 mm |
| dedendum della ruota dentata | $$t_f = 1.25 \cdot m $$ | 6.25 mm |
| spessore del dente misurato sulla circonferenza primitiva | $$s = \frac{m \cdot \pi}{2} $$ | 7.85 mm |
| $$z_{min} = 1.25 \cdot \frac {2} {{sin}^2(\alpha)} $$ | 22 | |
| addendum dell'utensile dentiera | $$h_a = 1.25 \cdot m $$ | 6.25 mm |
| dedendum dell'utensile dentiera | $$h_f = 1.25 \cdot m $$ | 6.25 mm |
| carico nominale, normale alla linea di contatto | $$F_{bn} = \frac {C} {d/2 \cdot cos(\alpha)} $$ | 3547.26 N |
| $$ \alpha_1 $$ | 26.92° | |
| componente del carico nominale, perpendicolare all'asse del dente | $$F_{bt} = F_{bn} \cdot cos(\alpha_1) $$ | 3162.85 N |
| spessore del dente alla sezione critica | $$ s_{Fn} $$ | 9.74 mm |
| braccio del carico applicato all'estremità del dente | $$h_{Fe} $$ | 9.4 mm |
| fattore di forma del dente - metodo di Lewis | $$Y_{L} = \frac {{s_{Fn}}^2} {6 \cdot h_{Fe} \cdot m} $$ | 0.3361 |
| sforzo massimo a flessione alla base del dente al punto T | $$\sigma_{f} = \frac {F_{bt}} {Y_L \cdot b \cdot m} $$ | 188.21 N/mm2 |
Rapporto di trasmissione
Il rapporto di trasmissione $\tau$ di una coppia di ruote dentate è il rapporto matematico dato dalla velocità angolare della ruota conduttrice diviso quella della
ruota condotta e si calcola con le seguenti formule:
$$\tau=\frac {\omega_1} {\omega_2}=\frac {d_2} {d_1}=\frac {z_2} {z_1}$$
dove
$\omega_1$ è la velocità angolare della ruota motrice e $\omega_2$ è la velocità angolare della ruota condatta;
$d_1$ è il diametro primitivo della ruota motrice e $d_2$ è il diametro primitivo della ruota condatta;
$z_1$ è il numero di denti della ruota motrice e $z_2$ è il numero di denti della ruota condatta.
Interasse
Per una coppia ruota-pignone senza correzione (x/m = 0) o nel caso di correzione complementare (ad esempio, pignone caratterizzato da uno spostamento positivo x/m = +0.5 e ruota corretta con x/m = -0.5), l'interasse tra le ruote $i$ viene calcolato con la seguente formula: $$i = \frac {d_1} {2} + \frac {d_2} {2} = \frac {m \cdot (z_1 + z_2)} {2} $$ Nel caso in cui $x_1+x_2\neq0$, l'interasse tra le ruote $i'$ è diverso da $i$ e può essere calcolato risolvendo le seguenti formule: $$ inv(\alpha')= \frac {2 \cdot (x_1+x_2) \cdot tan(\alpha)} {m \cdot (z_1 + z_2)} + inv(\alpha)$$ $$i'=i\cdot\frac {cos(\alpha)} {cos(\alpha')}$$ dove $ \alpha' $ è l'angolo di pressione durante il funzionamento, diverso dall'angolo di pressione $ \alpha $ dell'utensile dentiera.
Gioco di testa
Il gioco di testa $c$ tra due ruote dentate dipende dal valore di $(x_1+x_2)$ e può essere calcolato con la formula: $$c=m\cdot\left[0.25-\frac {x_1+x_2} {m}+\frac {z_1+z_2} {2}\cdot \left( \frac {cos(\alpha)} {cos(\alpha')}-1\right)\right]$$ Per ruote dentate con $x_1+x_2=0$, il gioco di testa è pari a 0.25m (profilo base dente dentiera tipo A – ISO 53:1998).
Risoluzione
Nel software, è possibile impostare la risoluzione del processo di generazione per inviluppo della ruota dentata.
Di seguito il significato e i relativi valori del parametro Risoluzione:
| Passo utilizzato con l'utensile dentiera per creare la ruota dentata | Numero di punti sul profilo ad evolvente del dente | |
| Bassa | 4 deg | 5 |
| Media | 2 deg | 10 |
| Alta | 1 deg | 20 |
Bibliografia
[1] - Georges Henriot - Ingranaggi - Trattato teorico e pratico - Vol. I e II - Tecniche Nuove - Ed. 1977
[2] - Lodovico Soria - Tecnica degli ingranaggi : trattato teorico-pratico di calcolo, correzione, dentatura, misura, trattamento termico, finitura e controllo ingranaggi cilindrici, elicoidali,
a catena, conici dritti e conici spiroidali - Editore Viglongo - Torino - Ed. 1971
[3] - prof. Paolo Righettini - Progettazione funzionale di sistemi meccanici - Ruote Dentate - Università degli Studi di Bergamo - Italy
[4] - ISO 6336-1:1996 - Calculation of load capacity of spur and helical gears - Part 1: Basic principles, introduction and general influence factors
[5] - ISO 6336-3:2006 - Calculation of load capacity of spur and helical gears - Part 3: Calculation of tooth bending strength
[6] - ISO 53:1998 - Cylindrical gears for general and heavy engineering - Standard basic rack tooth profile
[7] - Gear - en.wikipedia.org/wiki/Gear
